Fraktalet

[gurax]

Ky shkrim ka marre shkas nga shkrimi dhe fotot e sjella ketu , qe pershkruajne qelizat nervore.

Pervecse ato jane pamje fantastike, mua me le nje mbrese te thelle edhe fakti qe rregullsia e paraqitur ne ato pamje eshte nje rregullsi familjare, e riperseritur edhe ne shume raste te tjera ne natyre. Nje pattern qe te kujton pemet, eshte nje lloj pattern universal i cili mund te modelohet shume thjesht matematikisht. Madheshtia e ketyre modeleve matematike eshte se me ndryshime shume te vogla fillestare, mberrihet ne rezultate finale shume te ndryshme nga njera tjetra, secila po aq mbreselenese sa tjetra.

Te tera hyjne ne nje grup ekuacionesh dhe paraqitjet e tyre grafike qe i quajme fraktale. Ne menyre specifike, keto jane "pemet fraktale".

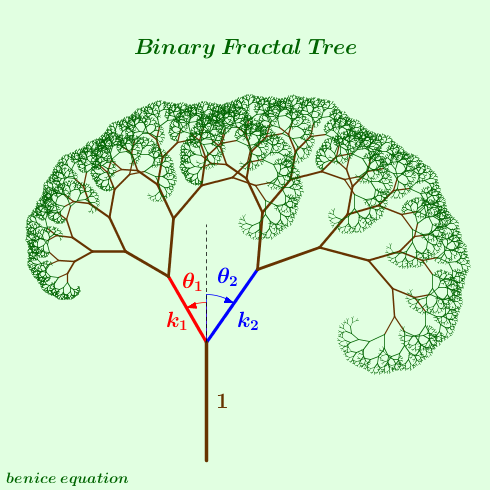
Ne parim pema fraktale eshte shume e thjeshte: Trungu baze ndahet ne dy dege. Secila nga keto dege ndahet perseri ne dy dege. Secila nga keto dege ndahet perseri ne dy dege. E keshtu perhere, pafundesisht.

Megjithate, ndryshime te vogla, ne dukje pa ndonje rendesi te vecante, do te cojne pamje shume te ndryshme nga njera tjetra.
Psh, gjatesia e cdo dege eshte sa gjysma e trungut ku ben pjese, te dy deget kane gjatesi te barabarte, dhe shperhapen ne menyre simetrike nga njeri tjetri.

Po sikur keto te mos jene keshtu?
Pamjet me poshte jane ndertuar nga ndryshime te vogla te parimit baze. Psh, kendi midis degeve nuk eshte i njejte ne te dy anet, ose gjatesia e degeve nuk eshte e njejte, apo kombinime te te dy ketyre faktoreve.

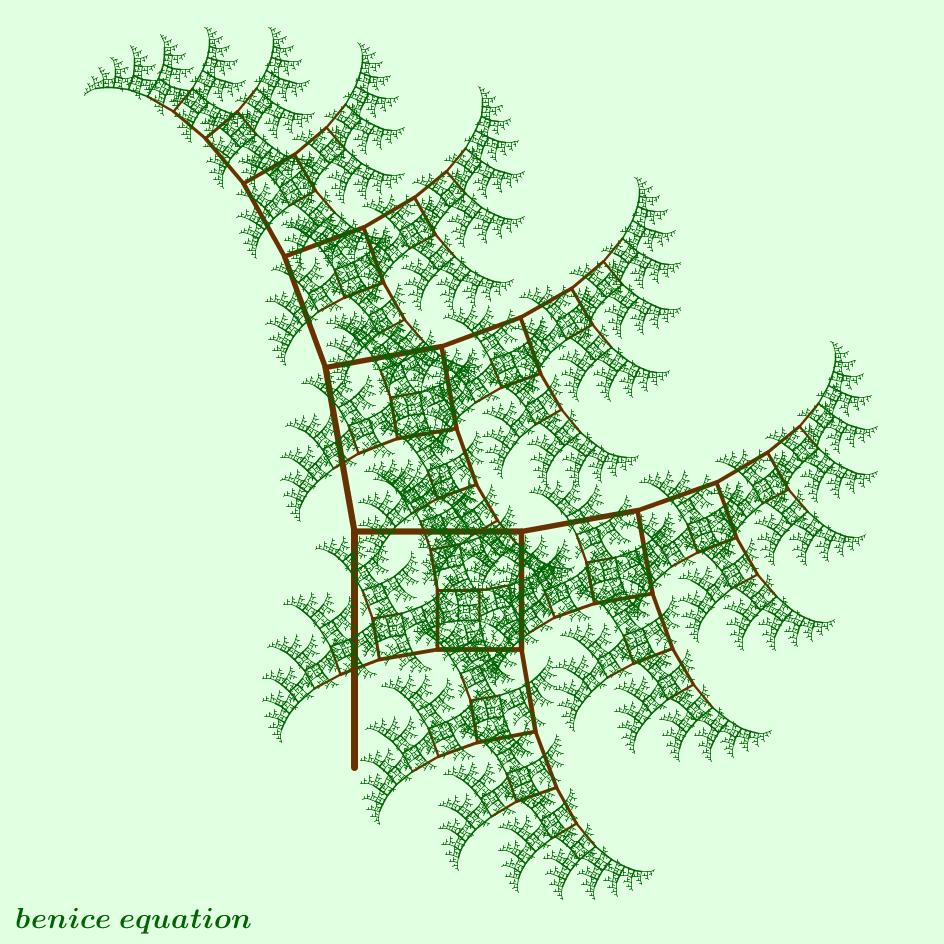
Nese fillojme shtojme elemenete - psh me shume sesa dy dege, apo nuk mjaftohemi me vizatim ne plan por nderfutim edhe dimensionin e trete dhe ndertojme keto fraktale ne hapesire, marrim pamje te ngjashme me keto:

Dhe duke marre per baze nje prej ketyre ketu me lart, nuk eshte shume e veshtire te merren perfundime si keto ketu:

Spoiler: Art bazuar tek pemet fraktale

Ketu jane permendur vetem pemet fraktale. Por fraktalet jane te shumellojshme. Dhe kjo eshte tema e dedikuar per fraktalet.

 

[katsune]

oh c'me ringjalle ca kujtime te bukura te gjimnazit me fraktalet, gurax shume e bukur tema (kur te kem kohe do shkruaj me shume).

 

[gurax]

Ky nje fraktal surreal i bere me kompjuter.

Ky nje fraktal real i bere ne menyre natyrore.

 

[katsune]

fraktalet jane figura gjeometrike jo konvencionale te cilat sherbejne per te "lexuar" ose "pershkruar" pikerisht format jo te rregullta te pranishme ne natyre, per te cilat gjeometria elementare euklidiane (ajo e trekendeshave, e rretheve, ...) eshte e pamjaftueshme. pra gjeometria fraktale pershkruan kompleksitetin e natyres. matematicieni francez Benoit Mandelbroit eshte shpikesi i kesaj gjuhe te re matematikore, ne vitet 60-70. qellimi i tij ishte te gjente nje fare rregulli aty ku te tjeret shikonin vec kaos.

vete termi fraktal ka prejardhjen nga latinishtja "fractus" qe perkthehet si "e ndare", "e fragmentuar", duke shprehur idene e copezimit, e parregullsise.
pjesa me e madhe e formave qe shohim ne natyre, qe jane familjare per syrin tone, jane fraktale, sic tregojne edhe figurat me lart me pemet, lulelakren, neuronet, por jo vetem...edhe malet, rete, floket e debores, etj.
te gjitha pjeset e riperseritura dhe perberese te nje fraktali kane te njejten forme ne te tera dimensionet por ne shkalle te ndryshme madhesie.

nje fraktal klasik shume i studiuar eshte trekendeshi i Sierpinskit: duke u nisur nga nje trekendesh barabrinjes brenda tij behet nje ndarje ne 4 trekendesha barabrinjes me te vegjel, me pas ndahen ne infinit 3 trekendeshat qe rrethojne trekendeshin ne qender.

eshte verifikuar qe ky model matematikor eshte i aplikueshem per te realizuar disa antena telefoni celular.

shembuj te tjere fraktalesh ne matematike jane:

trekendeshi i Tartalies

pluhuri i Cantorit

Julia set

sot fraktalet perdoren per te studiuar organizmat e detit, frakturat si pasoje e termeteve, shfaqjen e vetetimave, levizjen e fluideve, etj...

 

[gurax]

Vertet broken_smile, B. Mandelbrot eshte ne rolin e babait te kesaj matematike te habitshme. Ka nje fraktal i cili permban emrin e tij, fraktali "Bashkesia e Mandelbrotit".

Eshte ne dukje kaq i thjeshte, por kur e sheh nga afer eshte shume me i bukur. Vetem duke ju afruar perhere e me teper zbulohet bukuria e vertete e tij.

 

[katsune]

wow vertet fantastike! edhe Escher disa vite para Mandelbrotit ka vizatuar (spontanisht?) dicka shume te ngjashme me fraktalet.


Circle Limit III

 

[Eléonoré]

Fraktalet jane forma te rregullta gjeometrike me simetri te perkryer te cilat mund te qendrojne te ndara nga njera tjetra duke krijuar nje ushtri te pafund te se njejtes gje. Po keshtu ato mund te kombinohen midis tyre ne nje forme te tille per te krijuar nje bashkesi krejt ndryshe dhe po aq te njejte me "vetveten" per hir te krijimit te formave perfekte.

Bukuria e fraktalit qendron ne aftesine e tij per te riprodhuar vetveten over and over again per arsye te informacionit qe memorja e tij ruan per "vetveten fillestare". Por debulesa ose pika me e dobet e fraktalit eshte rrezikshmeria qe i paraqitet origjinalit ose "babait" te tij. Ne qofte se origjinali zhduket atehere te gjitha kopjet e tij do te zhduken automatikisht.

Shembulli me i mire qe mund te jap ne lidhje me fraktalin eshte agjenti Smith tek filmi Matrix. Zoti Smith edhe pse paraqitet me nje ushtri te tere te vetvetes, ne lufte me Neon, eshte shume here me vulnerabel per arsye te asaj qe permenda.

Nje njeri qe riprodhon vetveten ne menyre te pafundme eshte nje njeri i cili nuk mund te ndahet ne pjeseza perberese. Edhe nese ai ndahet ne pjeseza ai eshte gjithnje ne gjendje te riperterihet dhe te vije ne formen e tij origjinale. Kjo eshte edhe ajo qe njihet me emrin fryma e shenjte. Aftesia e saj per te qendruar e papercare dhe per te rikrijuar vetveten pavaresisht situates e ben ATE si qenien me te rendesishme te Universit.


Adea